संवेग संरक्षण का नियम (Law of conservation of momentum)
'यदि एक या एक से अधिक वस्तुओं के निकाय (System) पर कोई असंतुलित बल कार्य न कर रहा हो तो निकाय का कुल संवेग संरक्षित (Conserve) रहता है।
अतः इसे संवेग संरक्षण का नियम कहा जाता है।'
संवेग संरक्षण के नियम के उदाहरण
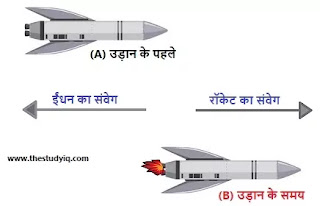
रॉकेट प्रणोदन (Rocket propulsion): रॉकेट का उड़ना न्यूटन के क्रिया-प्रतिक्रिया नियम तथा संवेग संरक्षण के सिद्धांत पर आधारित है।
रॉकेट का ईंधन (गैसें) जब जलता है तो यह क्रिया (Action) स्वरूप बाहर निकलती है तथा जब ये गैसें ज़मीन से टकराती हैं तो इस क्रिया की प्रतिक्रिया' रॉकेट को ऊपर की ओर धकेलती है।
रॉकेट के ईंधन का नियत वेग से दहन होने पर संवेग परिवर्तन की दर भी नियत (Constant) रहती है पर जैसे-जैसे रॉकेट उड़ता है, उससे निकलने वाली गैसों व ईंधन का द्रव्यमान कम होने के कारण, रॉकेट के वेग व त्वरण में वृद्धि हो जाती है। बंदूक से गोली छोड़ते समय बंदूक द्वारा गोली को एक वेग प्रदान कर दिया जाता है, जिससे गोली में आगे की दिशा में एक संवेग उत्पन्न हो जाता है। क्रिया-प्रतिक्रिया नियम के अनुसार गोली भी बंदूक को पीछे की ओर धकेलती है, जिससे बंदूक को भी पीछे की दिशा में एक संवेग प्राप्त हो जाता है।
यदि बंदूक चलाते समय बंदूक को शरीर (कंधे) से सटाकर रखा जाए तो निकाय (बंदूक + शरीर) का द्रव्यमान बढ़ जाने से संवेग भी बढ़ जाता है, जिससे गोली छूटने पर शरीर को पीछे की तरफ बहुत अधिक धक्का नहीं लगता है।
यदि समान द्रव्यमान की गोलियाँ दो अलग-अलग हल्की व भारी द्रव्यमान वाली बंदूकों से छोड़ी जाएँ तो भारी बंदूक से गोली दागते समय पीछे की तरफ धक्का कम लगेगा, जिससे कम चोट लगने की संभावना होगी।
जब विरामावस्था से आरंभ करके (शून्य संवेग) दो समान द्रव्यमान की गेंदें, समान वेग से चलना शुरू करती हैं अर्थात् दोनों वस्तुओं का संवेग समान है, यदि इन गेंदों की आपस में टक्कर हो जाए तो गति करती हुई गेंदें अचानक रुक जाती हैं अर्थात् संवेग पुनः शून्य हो जाता है अर्थात् 'टक्कर से पूर्व कुल संवेग = टक्कर के बाद कुल संवेग।'
संवेग संरक्षण के कारण ही जब कोई मनुष्य किसी स्थिर नाव से आगे कूदता है तो नाव पीछे खिसकती है। यदि मनुष्य का द्रव्यमान mM और नाव का द्रव्यमान mB है तथा मनुष्य VM के वेग से आगे कूदा तो संवेग संरक्षण के सिद्धांत के कारण ही नाव के पीछे खिसकने की चाल :
- यदि कोई मनुष्य किसी पूर्णतः घर्षणहीन पृष्ठ पर खड़ा हो तो केवल सीटी बजाने या जूते उतारकर एक दिशा में फेंकने से ही वह स्वयं को विपरीत दिशा में गति में ला सकता है।
या
संवेग संरक्षण का नियम samveg sanrakshan ka niyam
न्यूटन के द्वितीय नियम के साथ संयोजन से न्यूटन के तृतीय नियम का एक बहुत ही महत्त्वपूर्ण परिणाम है।
संवेग-संरक्षण (Conservation of momentum) के नियम के अनुसार एक या एक से अधिक वस्तुओं के निकाय (System) पर कोई बाहरी बल नहीं लग रहा हो, तो उस निकाय का कुछ संवेग नियत रहता है, अर्थात् संरक्षित रहता है।
रॉकेट प्रणोदन (Rocket propulsion) किसी रॉकेट की उड़ान उन शानदार उदाहरणों में से एक है जिनमें न्यूटन का तीसरा नियम या संवेग-संरक्षण नियम स्वयं को अभिव्यक्त करता है। इनमें ईंधन की दहन से पैदा हुई गैसें बाहर निकलती हैं और इसकी प्रतिक्रिया रॉकेट को धकेलती है।
संवेग का संरक्षण
प्रायोगिक तौर पर यह पुष्टि की जा चुकी है कि जब दो वस्तुओं में अन्योन्य - क्रिया होती है तो इन वस्तुओं के संवेग का सदिश योग परिवर्तित नहीं होता बशर्ते कि वस्तु पर कार्य कर रहा बल एकमात्र अन्योन्य क्रिया का बल ही हो। इसे संवेग संरक्षण का नियम कहते हैं। दो से अधिक वस्तुओं की अन्योन्य क्रिया के लिए भी यही तथ्य सही पाया गया है। सामान्यतः परस्पर अन्योन्यक्रियाशील अनेक वस्तुएं एक तंत्र बनाती हैं। यदि एक तंत्र की वस्तुएं तंत्र से बाहर की वस्तुओं के साथ अन्योन्य क्रिया नहीं करती तो तंत्र को संवृत तंत्र या वियुक्त तंत्र कहा जाता है।
इससे यह निष्कर्ष निकलता है कि वियुक्त तंत्र बनाने वाली वस्तुओं का कुल संवेग तो अपरिवर्तित रहता है, लेकिन उस तंत्र के अवयवों के संवेगों के परिमाण या दिशा अथवा दोनों, अन्योन्य क्रिया के अनुसार परिवर्तित हो सकते हैं। वियुक्त तंत्र में वस्तु विशेष में संवेग परिवर्तन होने के क्या कारण हैं? रैखिक संवेग संरक्षण का नियम विभिन्न क्षेत्रों में बहुत सी परिघटनाओं पर लागू होता है जैसे संघट्टन, विस्फोट, नाभिकीय अभिक्रिया, रेडियोएक्टिव क्षय आदि।
न्यूटन के नियमों के परिणामस्वरुप संवेग संरक्षण
न्यूटन के द्वितीय गति नियम के अनुसार। जब वस्तु पर समय के लिए बल F कार्य करता है तो वस्तु के संवेग में परिवर्तन Δp का मान निम्न होता है:
Δp = F Δt
इससे यह स्पष्ट होता है कि यदि वस्तु पर कोई बल कार्य नहीं करता तो वस्तु के संवेग में परिवर्तन शून्य होगा अर्थात संवेग स्थिर रहेगा। यह स्पष्टीकरण वस्तुओं के तंत्र पर भी लागू किया जा सकता है। इसी परिणाम पर पहुँचने के लिये न्यूटन के तृतीय नियम का भी प्रयोग किया जा सकता है। दो वस्तुओं A और B के वियुक्त तंत्र (Isolated system) पर विचार करें जो समय के लिये अन्योन्य क्रिया करते हैं। यदि माने कि वे एक दूसरे पर FAB और FBA बल लगाती हैं तो न्यूटन के तृतीय नियम के अनुसार
अतः तंत्र के संवेग में कोई परिवर्तन नहीं होता है। दूसरे शब्दों में तन्त्र का संवेग संरक्षित रहता है।
संवेग संरक्षण के कुछ उदाहरण
बन्दूक का प्रतिक्षेप : जब बन्दूक से गोली चलायी जाती है तो बन्दूक प्रतिक्षेप करती है। बन्दूक के प्रतिक्षेप वेग υ2 को संवेग संरक्षण के नियम से प्राप्त किया जा सकता है। यदि M द्रव्यमान की बन्दूक से चली गोली का द्रव्यमान m मानें और गोली का वेग υ1 हो और बन्दूक का वेग υ2 हो तो संवेग संरक्षण के नियम के अनुसार
mυ1 + Mυ2 = 0
यहाँ पर ऋण चिन्ह दर्शाता है कि υ2 और υ1 एक दूसरे की विपरीत दिशा में हैं। सामान्यतः m << M, बन्दूक का प्रतिक्षेप वेग गोली के प्रतिक्षेप वेग से बहुत कम होता है।
संघट्ट : संघट्ट में हम टकराने वाली वस्तुओं को एक तंत्र का अंश मान सकते हैं। संघट्टनशील वस्तुओं पर किसी प्रकार के बाह्म बल माना जा सकता है। संघट्ट करती वस्तुओं पर किसी प्रकार के बाह्य बल जैसे कि घर्षण बल की अनुपस्थिति में तंत्र को वियुक्त तंत्र (isolated system) माना जा सकता है। संघट्ट करती वस्तुओं के बीच अन्योन्य क्रिया के कारण इनका कुल संवेग अपरिवर्तित रहता है।
कैरम में स्ट्राइकर और गोटियों के बीच और बिलियर्ड में गेंदों के बीच संघट्टन प्रत्यास्थ वस्तुओं के बीच संघट्ट के अध्ययन में बहुत शिक्षाप्रद सिद्ध हो सकते हैं।
उदाहरण : दो परस्पर संयुक्त ट्रालियाँ जिनमें से प्रत्येक का द्रव्यमान m है प्रारंभिक वेग υ से चल रही हैं वे m द्रव्यमान वाली B तीन स्थिर ट्रालियों के साथ टकराकर उसी दिशा में चलती रहती हैं। संघट्ट के बाद ट्रॉलियों का वेग क्या होगा?
हल : संघट्ट के बाद ट्रॉलियों का वेग υ' मानते हैं।
संघट्ट से पहले संवेग = 2 mυ
संघट्ट के पश्चात संवेग = 5 mυ'
बम विस्फोट : संचित ऊर्जा के मुक्त होने पर बम स्फिोटित होकर खंड-खंड हो जाता है। प्रारम्भ में स्थिर रखे एक बम पर विचार करें जिसका A और B दो खण्डों में विस्फोट होता है। विस्फोट से पहले बम का संवेग शून्य था, विस्फोट के बने दोनों खंडों का कुल संवेग भी शून्य होगा। इस कारण से दोनों अंश विपरीत दिशा में समान संवेग से उड़ेगे। यदि दोनों खण्डों के दव्यमान समान हों, तो दोनों खण्डों के वेगों के परिमाण भी समान होंगे।
राकेट नोदन : एक राकेट की उड़ान संवेग संरक्षण का महत्पूर्ण व्यावहारिक अनुप्रयोग है। राकेट में ईंधन टैंक युक्त एक कोश होता है जिसे एक निकाय माना जा सकता है। कोश में एक नोजल होता है जिसके द्वारा उच्च दाब पर गैसों का निष्कासन होता है। जब राकेट को फायर करते हैं तो इंधन का दहन बहुत अधिक दाब और ताप पर गैसें उत्पन्न करता है। उच्च दाब के कारण ये गैसें अति उच्च वेग से नोजल से निकलती हैं जिसके कारण राकेट का द्रव्यमान M और प्रति सेकंड निष्कासित होने वाली गैस का द्रव्यमान m व वेग υ हो तो τ सेकंड में गैस के संवेग में परिवर्तन = mυτ.
यदि τ सेकन्ड में रॉकेट के वेग में वृद्धि V हो तो इसके संवेग में वृद्धि = MV संवेग संरक्षण के सिद्धांत के अनुसार

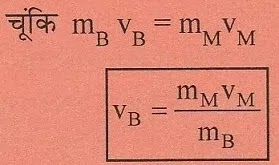




Very nice
ReplyDeleteVery nice
ReplyDelete